Motivating Example
Calculating return is important to evaluate a policy. 因此,为了比较以下三个策略,利用Discounted Return,很容易分析得,第一个策略是最好的。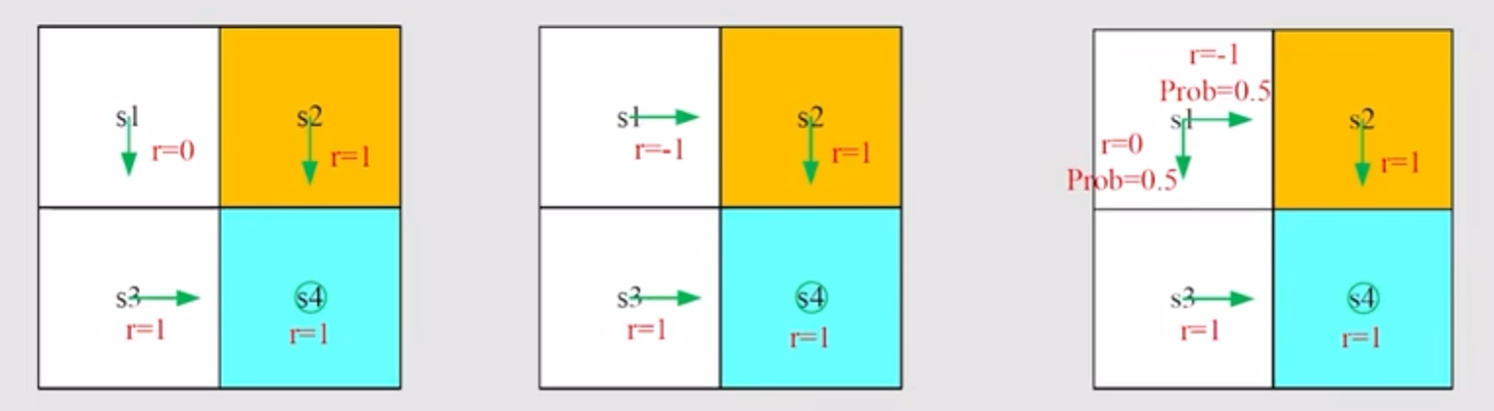
对于第三个策略的Return,其实是一种期望。这可以作为理解Bellman Equation的一个引子。
Bootstrapping
Bootstrapping是一种计算Discounted Return的办法。设置一个较为简单的循环policy作为演示: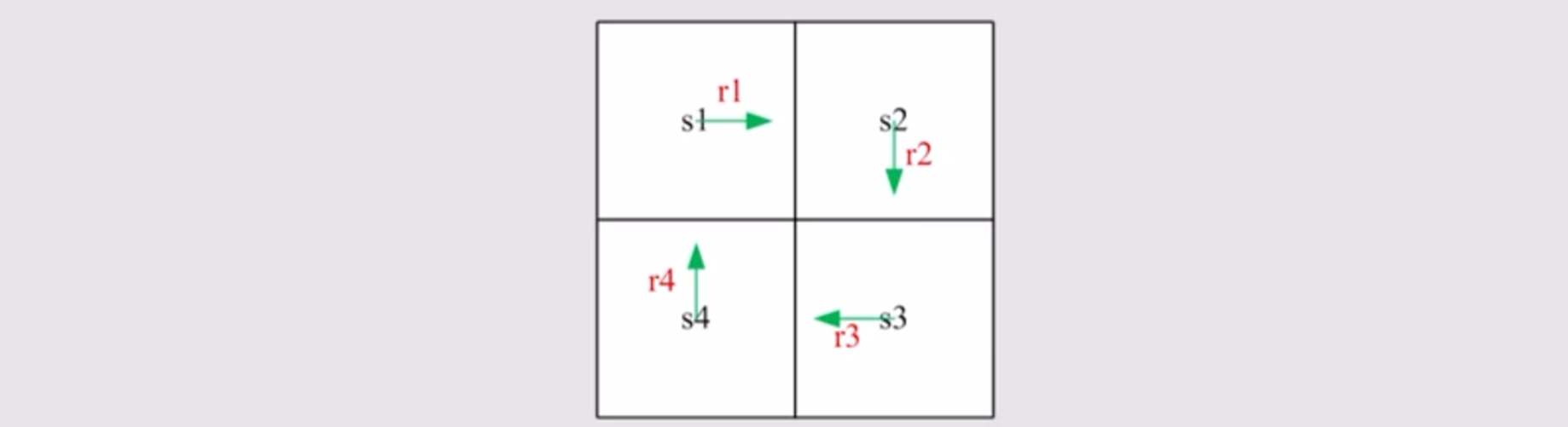
根据Discounted Return的定义,可以列出:
\[
\begin{align}
v_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + \dots \\
v_2 = r_2 + \gamma r_3 + \gamma^2 r_4 + \dots \\
v_3 = r_3 + \gamma r_4 + \gamma^2 r_1 + \dots \\
v_4 = r_4 + \gamma r_1 + \gamma^2 r_2 + \dots \\
\end{align}
\]
仔细观察之后,可以发现有一种整体替代的办法,把无穷项化为有限项:
\[
\begin{align}
v_1 = r_1 + \gamma v_2 \\
v_2 = r_2 + \gamma v_3 \\
v_3 = r_3 + \gamma v_4 \\
v_4 = r_4 + \gamma v_1 \\
\end{align}
\]
这种办法可以用矩阵表达,如下:
\[
\begin{pmatrix}
v_1 \\
v_2 \\
v_3 \\
v_4 \\
\end{pmatrix}
=\begin{pmatrix}
r_1 \\
r_2 \\
r_3 \\
r_4 \\
\end{pmatrix}+\gamma
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 \\
\end{pmatrix}
\begin{pmatrix}
v_1 \\
v_2 \\
v_3 \\
v_4 \\
\end{pmatrix}
\]
也可以写作:
\[
\textbf{v} = \textbf{r} + \gamma \textbf{Pv}
\]
这其实就是对于deterministic cases的Bellman Equation,它的解为:
\[
\textbf{v} = (\textbf{I} - \gamma \textbf{P})^{-1}\textbf{r}
\]
这种整体替代的办法就是Bootstrapping,其核心就是每一个state的Discounted Return依赖于其他state的Discounted Return。
State Value
这一小节当中,我们要从deterministic cases过渡到stochastic cases中去,对于这两种情况,强化学习的各种概念的含义是保持一致的,只是每一个定量都变为了随机变量。而相应的,Discounted Return的概念要过渡到State Value,这是强化学习最核心的概念之一。
Notations
把RL中的定量重新定义成随机变量,考虑MDP中的一步:
\[
S_t \xrightarrow{A_t} R_{t+1}, S_{t+1}
\]
- $t$, $t+1$表示离散化的时间。
- $S_t$ 表示时间$t$时,agent的状态。
- $A_t$ 表示时间$t$时,agent的所采取的行动。
- $R_{t+1}$ 表示时间$t$时,agent的状态从$S_t$迁移至$S_{t+1}$所获得的奖励,有时也写作$R_{t}$.
注意,$S_t$, $A_t$, $R_{t+1}$均是随机变量。这一步演化过程受概率分布的控制。 - $ S_t \xrightarrow{} A_{t} $ is governed by $\pi(A_t = a | S_t = s)$
- $ S_t, A_{t} \xrightarrow{} R_{t+1} $ is governed by $p(R_{t+1} = r | S_t = s, A{t} = a)$
- $ S_t, A_{t} \xrightarrow{} S_{t+1} $ is governed by $p(S_{t+1} = s’ | S_t = s, A{t} = a)$
这里有一个很有趣的问题,既然演化过程中所采取的行动、下一步的状态、所获得奖励都受概率分布的控制,那么我们为什么不统一地用$p(\dots | \dots)$表达,而对于策略专门用了$\pi$表示呢?笔者思考了一下,认为决定的所采取的行动的策略($\pi(A_t = a | S_t = s)$)从本质上不同于$p(R_{t+1} = r | S_t = s, A{t} = a)$, $p(S_{t+1} = s’ | S_t = s, A{t} = a)$. 后两者描述的是agent采取行动之后环境与agent的交互情况,这实际上是取决于环境本身(比如grid-world当中网格的构造,哪里是target area,哪里是forbidden area)以及人们基于训练目标所设定的激励政策。这些内容可能在一定程度上是固定的(比如一个trajectory中),虽然其分布有可能知道,也有可能不知道(后面会解释)。而策略$\pi$则完全由agent学习而得,在学习过程中应当是不断变化的,才能取得进步。
Definition of State Value
考虑一个trajectory:
\[
S_t \xrightarrow{A_t} R_{t+1}, S_{t+1} \xrightarrow{A_{t+1}} R_{t+2}, S_{t+2} \xrightarrow{A_{t+2}} R_{t+3}, S_{t+3} \dots
\]
Discounted Return 是:
\[
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \dots
\]
显然,$R_{i}$是一个随机变量,那么$G_t$也是一个随机变量。而它的期望就被定义为在状态$s$下,基于策略$\pi$的State Value: $v_{\pi}(s)$.
\[
v_{\pi}(s) = \mathbb{E}[G_t | S_t = s]
\]
- State Value 是关于状态$s$的函数,评价了一个状态的价值。
- State Value 也是策略$\pi$的函数,它的评价是基于目前选择的这个策略的。状态给定的情况下,基于某一个策略得到的State Value更高,证明这个策略更好,follow这条策略更有可能得到更高的return.
- Discounted Return 和 State Value 的关系:对于 deterministic cases, Discounted Return 和 State Value 没有区别,而对于 stochastic cases, State Value 就是 Discounted Return 的期望。
Establishment of Bellman Equation
由上一小节,Discounted Return 是:
\[
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \dots
\]
使用Bootstrapping方法,可得:
\[
G_t = R_{t+1} + \gamma G_{t+1}
\]
再结合State Value的定义,可得:
\[
\begin{align}
v_{\pi}(s) & = \mathbb{E}[G_t | S_t = s] \\
& = \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t = s] \\
& = \mathbb{E}[R_{t+1} | S_t = s] + \gamma \mathbb{E}[G_{t+1}| S_t = s]\\
\end{align}
\]
下面分别计算:
\[
\begin{align}
\mathbb{E}[R_{t+1} | S_t = s] = \sum \limits_{a}^{} \pi(a | s) \sum \limits_{r} r \cdot p(r | s, a)
\end{align}
\]
\[
\begin{align}
\mathbb{E}[G_{t+1}| S_t = s] & = \sum \limits_{s’} \mathbb{E}[G_{t+1}| S_t = s, S_{t+1} = s’] p(s’|s) \\
& = \sum \limits_{s’} \mathbb{E}[G_{t+1}| S_{t+1} = s’] p(s’|s) \\
& = \sum \limits_{s’} v_{\pi}(s’) p(s’|s) \\
& = \sum \limits_{s’} v_{\pi}(s’) \sum \limits_{a} p(s’|s, a) \pi(a|s) \\
\end{align}
\]
因此:
\[
\begin{align}
v_{\pi}(s) & = \mathbb{E}[R_{t+1} | S_t = s] + \gamma \mathbb{E}[G_{t+1}| S_t = s]\\
& = \sum \limits_{a}^{} \pi(a | s) \sum \limits_{r} r \cdot p(r | s, a) + \gamma \sum \limits_{a} \pi(a|s) \sum \limits_{s’} v_{\pi}(s’) p(s’|s, a) \\
& = \sum \limits_{a}^{} \pi(a | s) \left[\sum \limits_{r} r \cdot p(r | s, a) + \gamma \sum \limits_{s’} v_{\pi}(s’) p(s’|s, a)\right] \\
\end{align}
\]
这就得到了Bellman Equation。
对于每一个状态均可以写出来一个Bellman Equation,因此,这一组方程不同状态的State Value之间的关系,即Bootstrapping方法。
Bellman Equation是基于策略$\pi(a|s)$的,因此,求解Bellman Equation又被称作policy evaluation.
$p(s’|s, a), p(r | s, a)$这两项指的是我们对于agent处于某一状态下,采取了某一行动之后,所获得奖励和所迁移到的下一状态的概率分布。我们对这个概率分布是否完全掌握,从本质上反映了我们对于与agent交互的环境是否有完全的了解(即Environment Model是否建立)。如果对所处的环境没有完全掌握,agent只能通过不断试验,观测所处的环境。从这一判断标准出发,强化学习可分为Model-Based RL和Model-Free RL.
Matrix-Vector Form of the Bellman Equation
Rewrite the Bellman Equation in Matrix-Vector Form
对Bellman Equation作如下代换:
\[
\begin{align}
r_{\pi}(s) = \sum \limits_{a} \pi(a|s) \sum \limits_{r} p(r|s,a) \cdot r \\
p_{\pi}(s’ | s) = \sum \limits_{a} \pi(a|s) p(s’|s,a)
\end{align}
\]
式中,$p_{\pi}(s’ | s)$是follow策略$\pi$下,从状态$s$迁移到$s’$的概率;$r_{\pi}(s)$是follow策略$\pi$下,状态$s$这一步得到奖励的期望。因此,可以将Bellman Equation写成:
\[
v_{\pi}(s_i) = r_{\pi}(s_i) + \gamma \sum \limits_{s_j} p_{\pi}(s_j | s_i) v_{\pi}(s_j)
\]
写成矩阵形式为:
\[
\textbf{v}_{\pi} = \textbf{r}_{\pi} + \gamma \textbf{P}_{\pi}\textbf{v}_{\pi}
\]
式中,$[\textbf{P}_{\pi}]_{ij} = p_{\pi}(s_j | s_i)$,被称为State Transition Matrix.
Solution of the Bellman Equation
从数学上,Bellman Equation的解可写作:
\[
\textbf{v}_{\pi} = (\textbf{I} - \gamma \textbf{P}_{\pi}) ^{-1} \textbf{r}_{\pi}
\]
而实际上,由于$\textbf{v}_{\pi}$常常维数很高,上面的逆矩阵很难用计算机求解,我们常采用迭代的方法求解:
\[
\textbf{v}_{k+1} = \textbf{r}_{\pi} + \gamma \textbf{P}_{\pi}\textbf{v}_{k}
\]
从数学上,可以证明这种迭代的方法下,最终会收敛到Bellman Equation的解(证明略)。