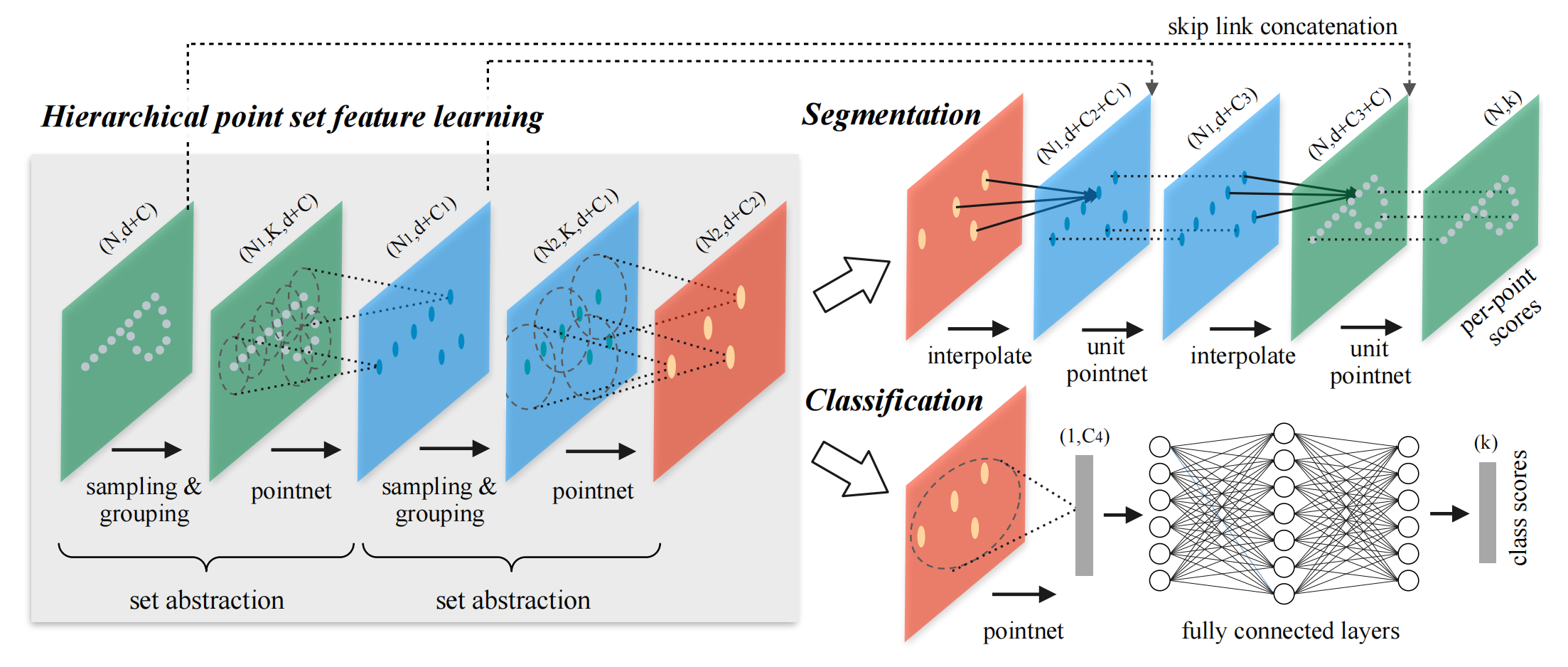
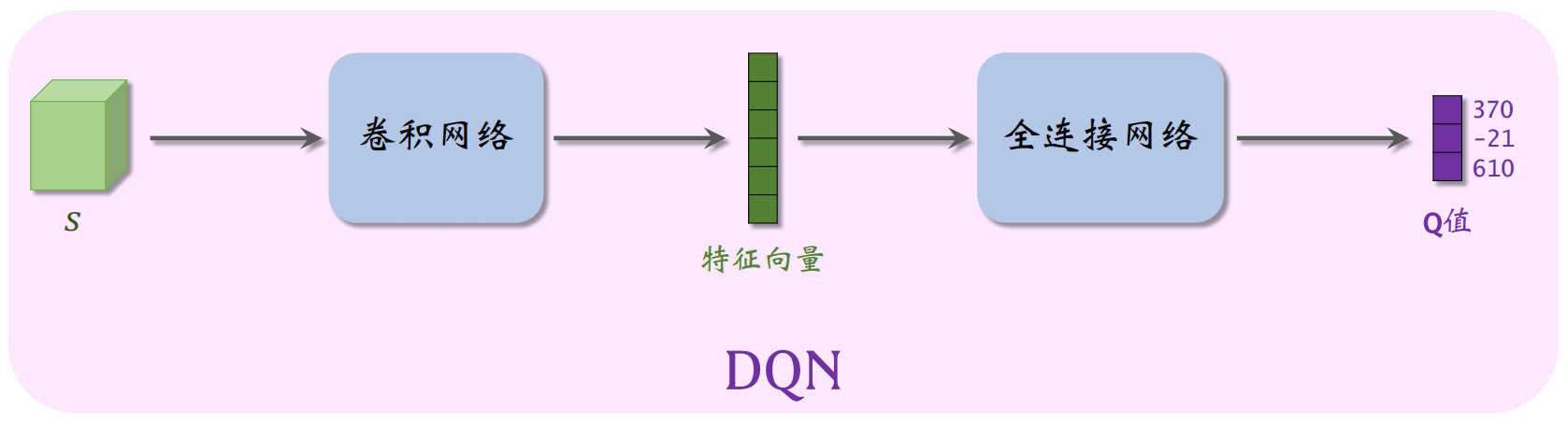
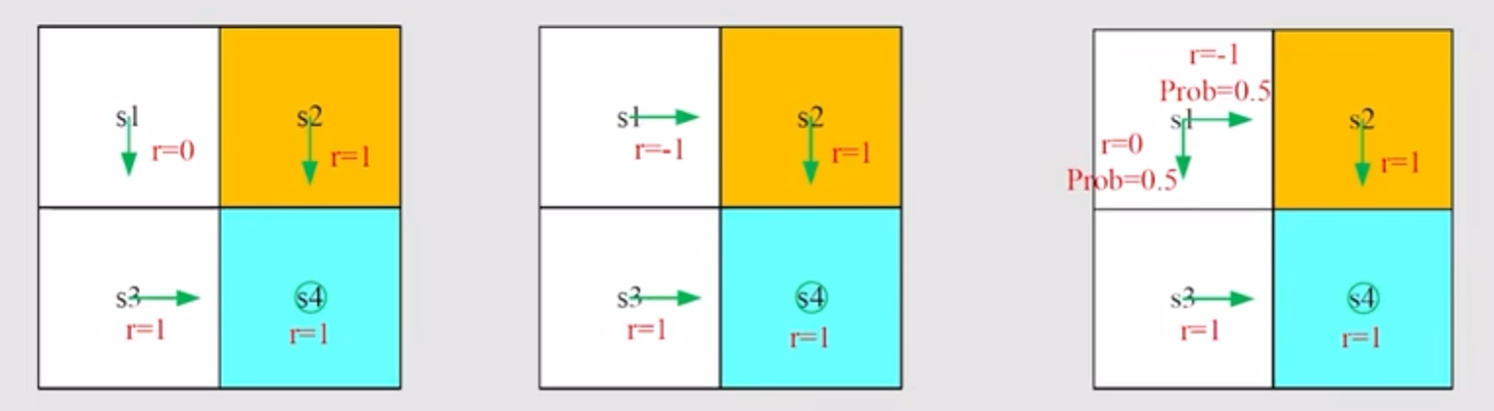
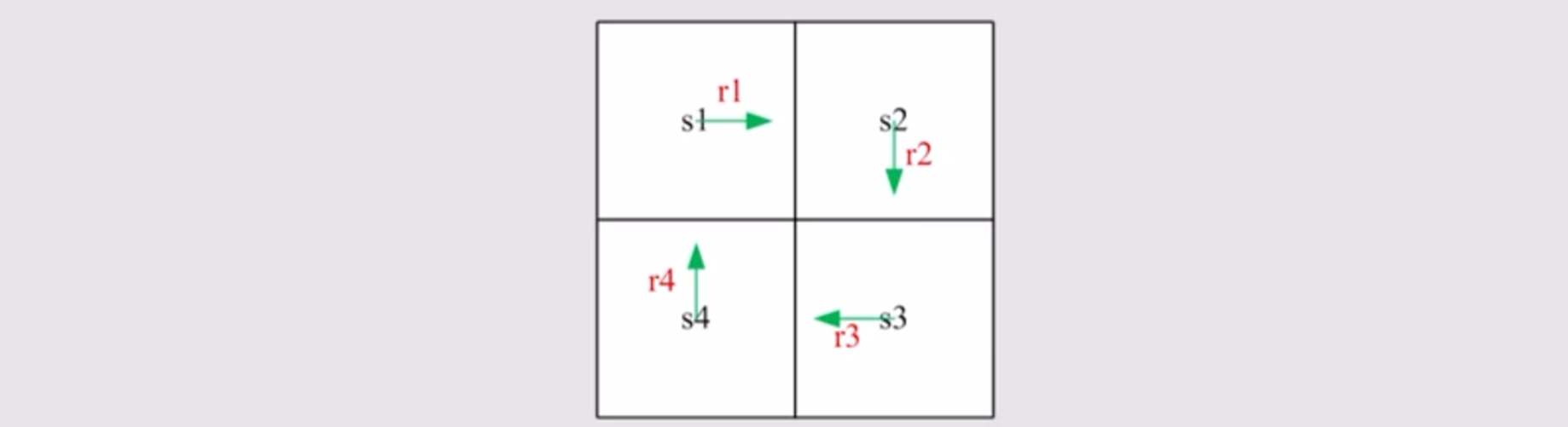
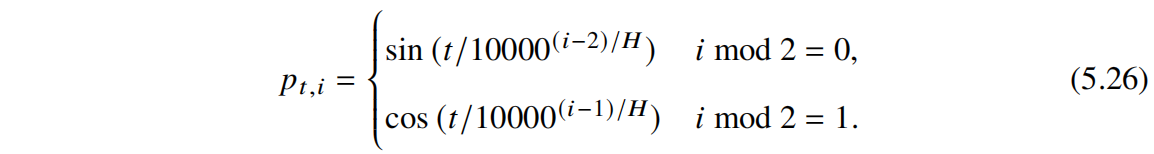Transformer
Transformer 架构由 Google 在 NIPS 2017 提出，之后成为各种大模型的基础架构。一个完整的 Transformer 由 Encoder 和 Decoder 组成，整个架构图如下：
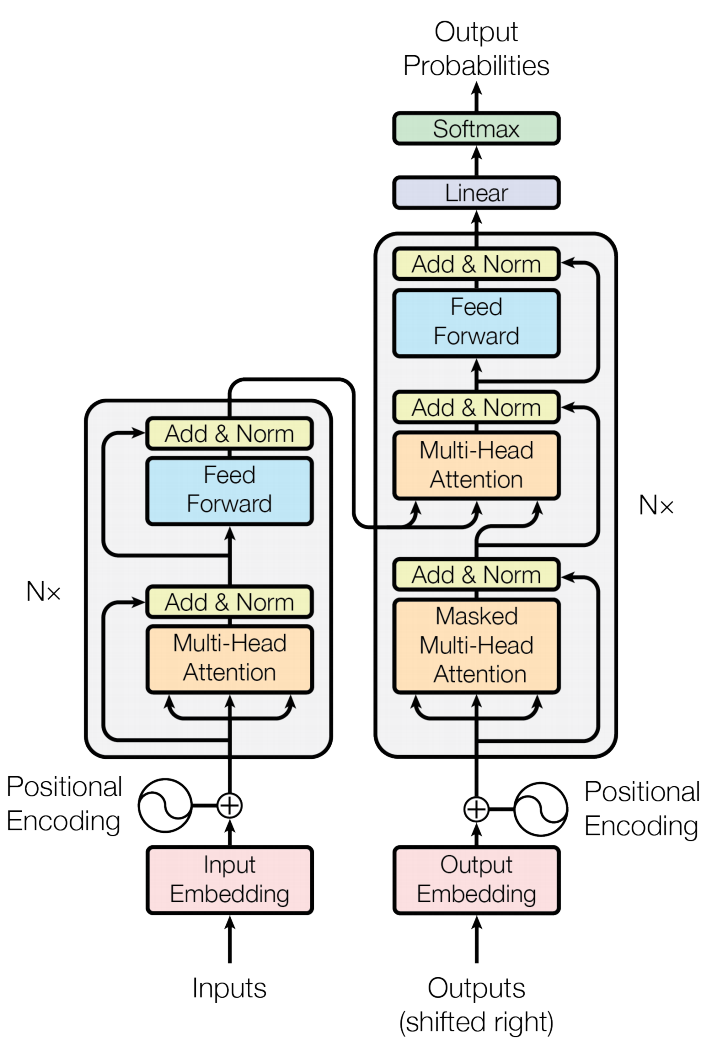
首先，整体概述 Transformer 的流程：
输入序列首先作 Input Embedding & Positional Embedding, 映射为矩阵，之后经过 $N$ 个 Encoder 子模块，每个模块都由 Self-Attention 和 Feed Forward Network 组成，并且每个模块后都进行残差连接和 LayerNorm. 最后得到整个 Encoder 模块的输出矩阵 $X$, 以待 Decoder 中 Cross-Attention 模块使用。
将已经输出的序列作 Output Embedding & Positioinal Embedding, 映射为矩阵，之后经过 $N$ 个 Decoder 子模块，每个模块都有一个 Masked-Attention, 一个 Cross-Attention, 一个 Feed Forward Attention 组成。同样每个模块之后都有残差连接和 LayerNorm.
最后解码器输出的结果经过线性映射，再经过 Softmax 映射为概率。从概率最大的几个 token 中按概率抽样，转为文本，输出。（取决于 top_p, temperature 等参数）
Embedding
Input Embedding
由于 Transformer 最早应用于机器翻译领域，这里以机器翻译为示例。输入是一长段文本，首先要进行 tokenize, 就是把一长串文本化为 token, 每一个 token 可能是一个单词，也可能长于一个单词（如固定搭配表示特殊的语义），也可能短于一个单词（如词根词缀也能表示一定的独立语义）。
Tokenize 之后，要对 token 进行 embedding, 就是把 token 映射到向量。这一步可以基于一个词表做，例如 Word2Vec. 不过训练较为复杂的模型时，初始的 embedding 词表其实并不重要，随机初始化的效果与基于 Word2Vec 的效果差别不大。
Positional Embedding
由于 Transformer 是把一串文本打散了之后输入，这样就会丢失某一个词在原始序列中的位置信息，因此在 Input Embedding 之后要做一步 Positional Embedding, 把初始的位置信息融入到嵌入向量中。具体公式如下：t 就是 token 在序列中的位置，i 表示 Positional Embedding 的第 i 维，H 表示 Embedding 的维数。
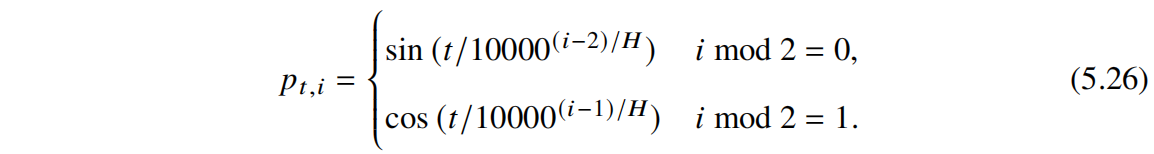
这样生成 Positional Embedding $p_k$ 与 Input Embedding $v_t$ 直接相加，得到总的 Embedding $x_t$. 这样输入从文本就转为一个矩阵 $x = [x_1, x_2,…, x_n]^T $.
Residual Connection
残差连接，就是把这一层的输出再加上这一层的输入。它旨在缓解梯度消失的问题，使得信息直接跨模块传递。
在梯度反向传播时，对于某一层的参数的偏导数，由于链式法则，是一系列偏导的乘积。连乘容易出现数值很小的情况，从而使参数更新缓慢，这一现象就是梯度消失。有了残差，求偏导就会多一个 1, 这样就避免了数值接近 0 的情况。
Normalization
Methods of Normalization
归一化的方法有很多，常见的有 BatchNorm, LayerNorm, RMSNorm, DeepNorm.
- BatchNorm (BN): 批次归一化，对于每次训练的 Batch，求得每一个维度的均值和标准差，进行缩放。然而对于小批量数据，这种用一个 Batch 的均值和标准差作为整体标准进行处理很容易误差较大，效果不好（NLP 任务中并不常用）。
\[
BatchNorm(x_i) = \frac{x_i - \mu_i}{\sigma_i} \cdot \gamma_i + \beta_i
\]
\[
\mu_i = \frac{\sum_j x_i^{(j)}}{BatchSize}, \sigma = \sqrt{\frac{\sum_j (x_i^{(j)} - \mu_i)^2}{BatchSize}}
\]
- LayerNorm (LN): 层归一化，对于每一个数据，求其所有维度数据的均值和方差进行缩放。这样每一个数据的缩放仅与自己有关，解决了 BN 在小样本上效果不佳的问题。
\[
LayerNorm(x) = \frac{x - \mu}{\sigma} \cdot \gamma + \beta
\]
\[
\mu = \frac{\sum x_i}{H}, \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{H}}
\]
- RMSNorm: RMS 归一化，可以看作是 Layer Norm 的变种，主要针对于 LN 要计算均值和标准差，计算量较大的问题。RMSNorm 直接令样本中每一个维度除以样本所有维度的方均值再缩放，RMSNorm 训练的速度和效果都比 LayerNorm 要好。
\[
RMSNorm(x) = \frac{x}{\sqrt{\sum x_i^2} } \cdot \gamma
\]
DeepNorm: 深度归一化，是一种 Post-Norm 方法，其实就是在残差连接中对之前的激活值 x 进行了缩放，残差计算之后再用 LayerNorm. MicroSoft 的研究人员发现这样的归一化可以使 Transformer 的训练更稳定，训练 1000 层以上的神经网络不再困难。
\[
DeepNorm(x) = LayerNorm( \alpha x + Sublayer(x))
\]
注：可以发现在 BN, LN, RMSNorm 中都有一些 learnable 参数（如 $\gamma, \beta$），这可以调整归一化的强度，未必彻底的归一化才适合。特别的，当 $\gamma = \sigma$, $\beta = \mu$ 时，相当于并没有归一化。
Position of NormLayer
归一化的位置也有很多种不同的选择，总结如下，其中每种归一化的优劣引用了《大语言模型》（赵鑫等）的总结：
Post-Norm: 后向归一化，最原始的Transformer中选择的是 Post-Norm，即一个 Sublayer(如 Attention, FeedForward) 之后做残差计算，残差之后再做归一化。
\[
PostNorm(x) = Norm(x + Sublayer(x))
\]
“在原理上，后向归一化具有很多优势。首先，有助于加快神经网络的训练收敛速度，使模型可以更有效地传播梯度，从而减少训练时间。其次，后向归一化可以降低神经网络对于超参数（如学习率、初始化参数等）的敏感性，使得网络更容易调优，并减少了超参数调整的难度。然而，由于在输出层附近存在梯度较大的问题，采用 Post-Norm 的 Transformer 模型在训练过程中通常会出现不稳定的现象。”Pre-Norm: 前向归一化，对 Sublayer 的输入做归一化，之后再过 Sublayer 层，算残差。
\[
PreNorm(x) = x + Sublayer(Norm(x))
\]“相较于 Post-Norm，Pre-Norm 直接把每个子层加在了归一化模块之后，仅仅对输入的表示进行了归一化，从而可以防止模型的梯度爆炸或者梯度消失现象。虽然使用了 Pre-Norm 的 Transformer 模型在训练过程中更加稳定，但是性能却逊色于采用了 Post-Norm 的模型。”
Sandwich-Norm: 三明治归一化，就是 Pre-Norm 和 Post-Norm 的结合，虽然想法比较理想，从理论上应该性能更好，但是实际中研究人员发现这种办法并不能使训练完全稳定，有时候甚至会崩溃。
\[
SandwichNorm(x) = x + Norm(Sublayer(Norm(x)))
\]
Feed Forward Neural Network
前馈神经网络，就是信息流动始终由前一层流向后一层，各层间信息没有反馈。比如 CNN, MLP 都属于前馈神经网络，而 RNN 不是。原始的 Transformer 这里用的是两层神经网络（两层的 MLP）。
Attention
Attention 机制是 Transformer 的独创性的重大突破，直接建模了任意距离的词元之间的语义关联，实现了在上下文中理解语义信息（解决了一词多义等问题），从而提高了模型理解复杂文本的能力。
Multi-head Attention
Multi-head Attention 计算过程：
先将输入矩阵 $X$ 映射为 $Q, K, V$:
\[
Q = X W^Q
\]
\[
K = X W^K
\]
\[
V = X W^V
\]
然后计算 Attention:
\[
Attention(Q, K, V) = Softmax(\frac{QK^T}{\sqrt{D}})V
\]
注意在 Decoder 中的 Attention 是 Masked-Attetion, 即要在计算 Attention 之前，把上三角元全部设为 -inf，这是因为使用词元预测的方法训练时，要使 Decoder 只能使用当前已生成的信息，而不能使用“未知”的信息。
在 Multi-head Attention 中，有 $N$ 组结构相同，而参数不同的 $W^Q, W^K, W^V$ 映射矩阵，把每一组参数作 Attention 之后的结果拼接起来，再通过一个矩阵映射得到最终的结果。
\[
head_i = Attention(XW^Q_i, XW^K_i, XW^V_i)
\]
\[
MHA(X) = Concat(head_1, head_2,…,head_n) W^O
\]
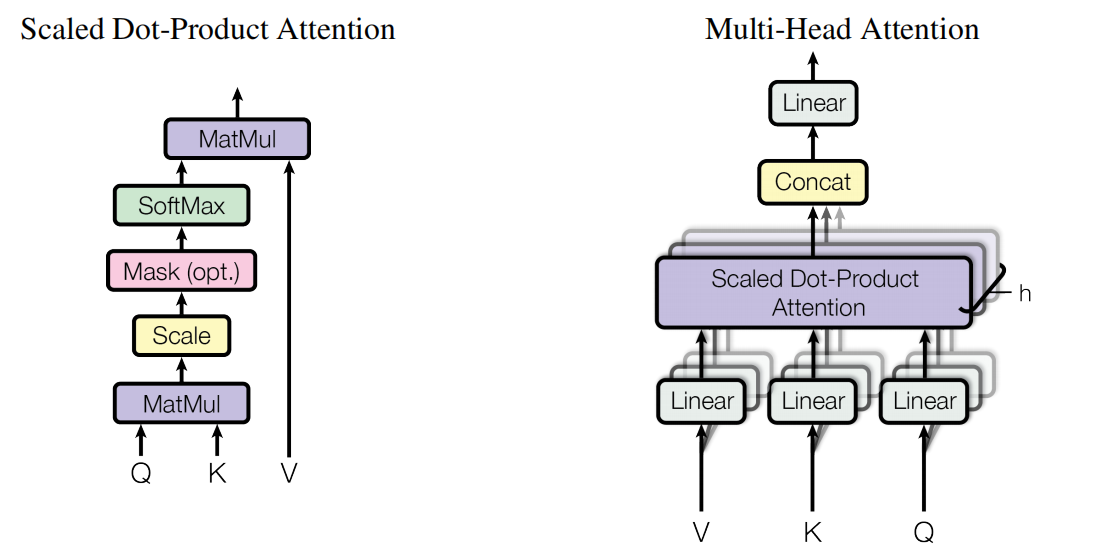
分析与解释：
- $K, Q, V$ 各自的含义？
$Q$ 表示当前查询的位置，$K$ 表示被查询的其他位置，$V$ 表示实际的语义信息。用 $Q$ 与 $K$ 点乘计算当前查询的位置与其他位置的相似度，再用 Softmax 转为概率，最后乘 $V$, 其实是各个位置语义信息作加权平均。 - 为什么用多头注意力？
（1）允许模型再不同位置联合处理表达不同子空间信息能力，增强非线性表达能力（将输入向量投影到不同的子空间中，每个子空间可能对应不同任务/特征，比如翻译任务中，有的头关注主谓一致，有的头关注动宾搭配，有的头关注主句和从句的关系等等）；
（2）缓解秩塌缩问题（有论文推导 Transformer 的秩表达式，多次注意力层堆叠后，注意力矩阵的秩逐渐降低至1，模型的表达能力退化，趋于固定分布），多头注意力可以将注意力矩阵的秩直接扩大 $N$ 倍，一定程度上可以缓解秩塌缩的问题。 - Attention 计算为什么除以 $\sqrt{D}$ ？
点积计算中数据随向量维度增大而增大，容易处在 Softmax 饱和区，梯度较小不易训练。
Self-Attention & Cross-Attention
Self-Attention, 自注意力，用于建模同一模态信息内部之间的关联，有助于理解文本的上下文语义。Self-Attention 中的 $K, Q, V$ 全部来自于 Input/Output.
Cross-Attention, 交互注意力，用于实现跨模态之间的语义对齐。Cross Attention 用在解码器中，$Q$ 来自于 Output, 而 $K,V$ 来自于 Input.
在 Decoder 中，每一个子模块先包含了 Masked-Self Attention, 这一模块用于理解已输出的信息，而此模块后续的 Cross-Attention 用于理解未输出的原始模态的信息（例如翻译任务，Masked-Self Attention 关注”It is a”, Cross Attention 关注“猫”）.
未完待续
Vision Transformer
Vision Transformer 旨在直接利用 Transformer 处理计算机视觉的任务，而不依赖于传统的 CNN。ViT 的主要思想是把一张图片打成 patch, 每一个 patch 相当于 NLP 任务中的一个 token. 这样就直接照搬 Transformer 中的 embedding, positional encoding, attention 等模块处理。
未完待续。
